Link operators allow you to insert matrix operations in the source to the destination matrix computation in order to offset the position, orientation, or scale of the destination object. For example, you may want to keep a node positioned in front of the view rather than directly on the view. Operators are implemented as position, orientation, or scale matrices that are multiplied with the source object's transform every frame.
Because operators work by performing matrix multiplication, the order in which the operator matrices are multiplied affects the outcome.
The difference between pre and post operations:
The pre operations are inserted to the left of source matrix in the link computation, while post operations are to the right. If matrix A is a pre operator, then it will multiply the source matrix, S, in this order: A * S. If A is a post operator, the multiplication order is reversed: S * A. The '*' character indicates matrix multiplication, not the dot product.
The formula for computing the destination matrix:
Destination = PreOps * Source * PostOps
When adding multiple operators to a link, order matters. Pre operators are always added to the beginning of the computation, before previous pre operations. Post operators are appended to the link computation. The basicLinking.py provides an example using pre operations to move the viewpoint over an avatar's shoulder.
The link computation for this example is: ViewTrans = E2*T1*E1*Source. Notice that the operators change the reference frame the of the previous operators. The reference frame of an operator/matrix is defined by the operator/matrix to the right.
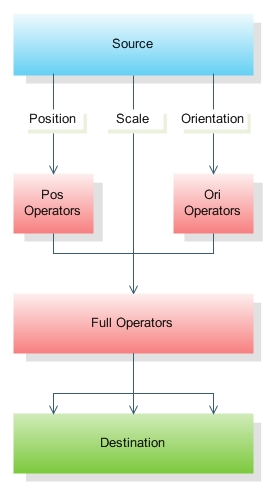
When computing the destination object's transform matrix, the link algorithm first gets the position and orientation matrices of the source, then it multiplies these together to produce a full position and orientation matrix. If you would like to apply an operation on the source's orientation or position matrix before they are combined in the full matrix, you can set the "target" parameter. As the third parameter in the pre and post methods, the target parameter can take viz.LINK_FULL_OP (default), viz.LINK_POS_OP, and viz.LINK_ORI_OP as possible arguments.
As an example, if we apply <link>.postEuler(0, 0, 90, viz.LINK_ORI_OP) then the destination matrix is rolled 90 degrees. Not only does this change orientation, but it also changes the position if the destination matrix has any translation. If we had called <link>.postEuler(0, 0, 90, viz.LINK_FULL_OP) then the matrix would simply roll the destination node 90 degrees without changing its position.
The pre and post methods of links return operator objects. You can use these objects to modify links after they have been created with the pre and post methods.
The following diagram illustrates the flow of data from the source object to the destination object
Linking Basics- Introduction to linking.
Advanced Linking - Discusses the implementation of links with matrix mathematics.
Link Command Table- List of relevant link commands.
Transform Basics- Introduces the position/orientation/scale matrix associated with all 3D nodes.