Vizard 8 » Reference » Basic Concepts » Understanding Coordinate Systems
8.0
In 3D space, the smallest area is a point. Each point is defined by a unique set of three numbers, called coordinates. An example point in 3D space would be (0,0,0), which defines the center point of 3D space. Each point in virtual space is specified by three numbers the representing horizontal, vertical, and depth components.
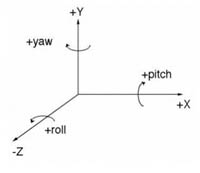
An axis is an imaginary line in space that defines a direction. There are three standard axes referred to as the X, Y, and Z axes, as shown in the figure here. As you can see, X is width, Y is height, and Z is depth. Note also the sign of the axes: positive X points to the right, positive Y points up, and positive Z points away or into the screen.
These axes are normally fixed relative to the world. The origin of the virtual universe is the intersection of the 3 axes. It's point is (0, 0, 0). This is the known as the world coordinate system. Each 3D model in the virtual world also has its own coordinate system which has its origin at the center of the object.
In Vizard, the linear unit of measurement is meters. This is especially important to remember when obtaining 3D models from 3rd party sources because their units may not be in meters, in which case the objects may appear extremely large or small when imported into Vizard.
When you start a blank world (e.g., issue the viz.go() command), the first view onto the world – your viewpoint – is what an observer would see while standing at the origin. The word "standing" here is important because the starting location of the viewpoint is exactly defined to be (0, 1.82, 0) meters. This means you are floating 6 feet (1.82 meters) over the origin (see <view>.eyeheight to adjust this default value).
The angular unit of measurement in Vizard is degrees. In the figure above, you'll notice three other terms are introduced: yaw, pitch, and roll. These are the standard terms for rotations about the respective axes: yaw rotations are around the y-axis, pitch rotations are around the x-axis, and roll rotations are around the z-axis. To remember which direction is a positive rotation for a given axis, imagine that your spine is aligned with the axis and your head is pointed in the positive direction. A rotation to your right would be a positive rotation about that axis.
Rotations and translations of a 3D node are applied within a specific frame of reference. That frame of reference can be the global frame of reference, the parent's frame of reference (if the node is a part of a hierarchy of nodes) or the local frame of reference. Rotations and translations can, furthermore, be applied relative to the current position and orientation of the node or absolutely.